במאמר שלהלן נבהיר אחת ולתמיד מהי סטיית תקן, מדוע מחשבים אותה מתוך שונות ואיך מחשבים סטיית תקן. כמו כן, נציג את ההבדל בין סטיית תקן מדגמית לעומת זו של האוכלוסייה. לבסוף, נדגים את השימושים השונים של סטיית תקן במחקר ובכלל ונסקור מספר דרכים פשוטות לחישובה.
תוכן עניינים

הגדרת שונות וסטיית תקן (Standard deviation)
כדי שנוכל להבין מהי סטיית תקן (Standard deviation, או בקיצור SD) נתחיל קודם בהגדרה הרשמית לשונות (Variance) ולאחר מכן נפרק ונפשט אותה.
שימו לב: למעשה ברגע שנדע איך מחשבים שונות ואיך להבינה, נדע זאת גם כלפי סטיית תקן.
ההגדרה הפורמלית לשונות היא: מדד פיזור לערכי ההתפלגות המשקף את ממוצע הסטיות הריבועיות מהממוצע. זו הגדרה שבדרך כלל מפילה מהכיסא, כך שאם נפלתם – תדעו שאתם לא לבד. מהניסיון שלנו, מרבית הסטודנטים לא מצליחים להבין מההגדרה הזו כמעט כלום ולכן נעבור צעד-צעד כדי שבעוד כמה רגעים תדעו בדיוק למה הכוונה.
נשתמש בדוגמה לשם המחשת ההגדרה, נחלק אותה לשלושה חלקים ונבין אותה מהסוף להתחלה:
הערכים בדוגמה הם: 1,3,5 – הבה נבחן מהי השונות של סדרת ערכים זו.
“מהממוצע”- כדי שנוכל לחשב את מידת הפיזור של סדרת הערכים אנחנו צריכים קודם לקבוע מהי נקודת הייחוס. כלומר, ביחס לאיזה ערך שאר הערכים בסדרה מפוזרים. הממוצע הוא הערך שביחס אליו בודקים את מידת הפיזור של הערכים ועל כן הצעד הראשון יהיה חישוב ממוצע של סדרת הערכים:
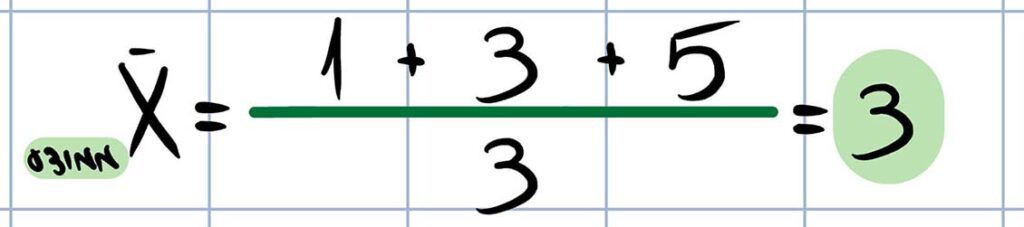
מצוין! כעת כשאנחנו יודעים מהו הממוצע של סדרת הערכים, נוכל להמשיך לחלק הבא של ההגדרה.
“סטיות ריבועיות מהממוצע”- סטייה, כשמה כן היא, מתייחסת למידה שבה סדרת הערכים סוטה מנקודת הייחוס, כלומר מהממוצע (שהוא 3 במקרה שלנו). במילים אחרות, זהו חישוב לפיו ניתן לקבוע באיזו מידה ערך כלשהו רחוק מהממוצע.
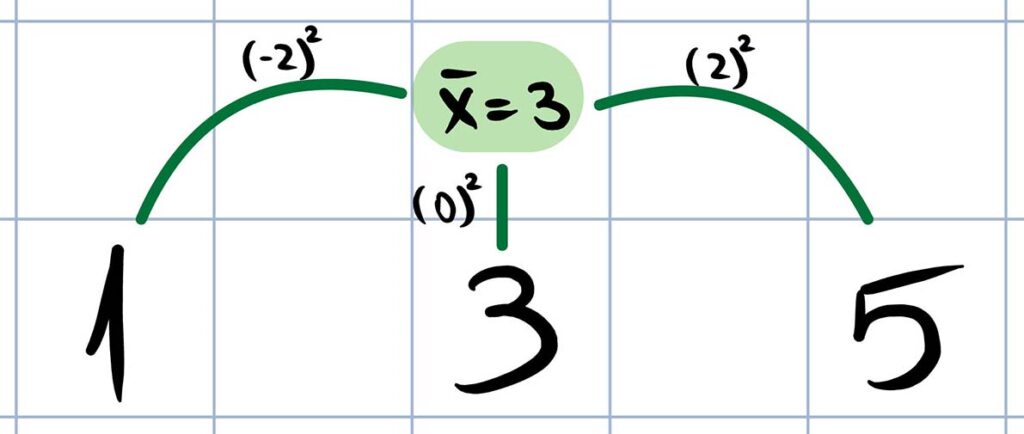
אם למשל נבדוק זאת על הערך הראשון בסדרת הערכים – 1, נוכל לראות שהוא רחוק ב-2 יחידות מהממוצע. הבעיה היא שכדי לחשב מרחק אנחנו משתמשים בנוסחה: 2-=1-3, לפיה מגלים שהערך 1 רחוק מהממוצע ב-2- יחידות. זו תקלה מכיוון שמרחק לא יכול להיות שלילי אלא חיובי בלבד. לדוגמה, המרחק מהבית שלי לסופר הוא 300 מטרים, ואילו המרחק מהסופר לבית שלי הוא גם 300 מטרים ולא 300- מטרים.
הפתרון לבעיה הוא שניתן להעלות בריבוע את המרחק השלילי שיצא בחישוב שערכנו ולקבל עבורו ערך חיובי מתאים: 4=2(1-3). כלומר, הסטייה הריבועית של הערך 1 מהממוצע היא 4. זו למעשה הסיבה שאנו מתייחסים לסטיות ריבועיות מהממוצע ולא רק על סטיות מהממוצע.
בנקודה זו אולי צצה לכם מחשבה – “רגע, אז למה להעלות בריבוע? בואו פשוט נהפוך את הסימן השלילי לחיובי – דהיינו, נחשב ערך מוחלט במקום להעלות את הסטייה מהממוצע בריבוע”. זו מחשבה לגיטימית בהחלט אולם היא לא לוקחת בחשבון שתי סיבות מרכזיות להעלאה בריבוע על פני שימוש בערך מוחלט:
- ריבוע הסטיות מהממוצע הופך את כל הסטיות לחיוביות ומבטל את הבעיה המתמטית שהייתה נוצרת לנוכח השימוש בסטיות מוחלטות.
- ריבוע הסטיות מדגיש את ההשפעה של ערכים חריגים (קיצוניים) בסדרת הערכים כפי שברצוננו לעשות בחישוב סטיית תקן ושונות.
כעת, נתייחס לביטוי הכולל והאחרון לשם הבנת ההגדרה.
“ממוצע הסטיות הריבועיות מהממוצע”- לאחר שחישבנו את מכלול הסטיות הריבועיות מהממוצע, נבצע עליהן חישוב ממוצע. זה מעט מבלבל כי זה נשמע כמו ממוצע בתוך ממוצע אך אם מציירים זאת רואים די בפשטות על מה מדובר. תחילה, נסכום את הסטיות הריבועיות של כל אחד מהערכים מהממוצע ולאחר מכן נחלק במספר הסטיות, כלומר ב-3 (שימו לב, מספר הסטיות תמיד שווה למספר הערכים בסדרה הואיל ולכל ערך ישנה סטייה מהממוצע):
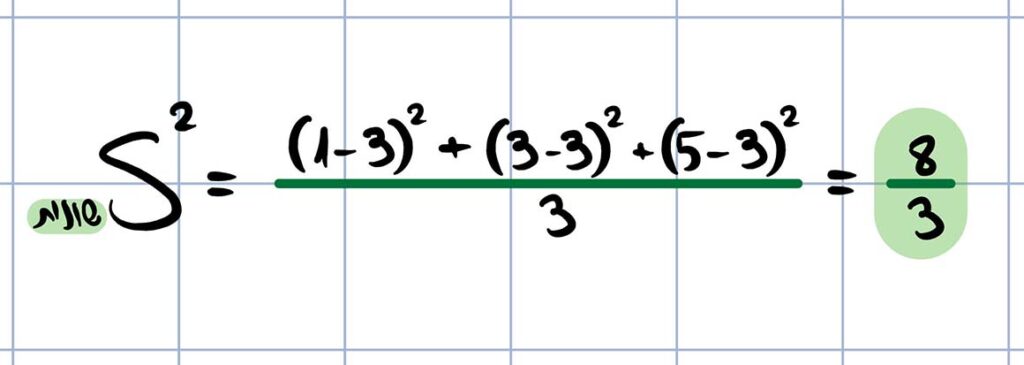
כפי שניתן לראות, השונות המסומנת באות (S2) שווה ל-8/3, כלומר ל-2.66.
נפלא! חישבנו שונות והצלחתם להבין למה הייתה הכוונה בהגדרה המאיימת לשונות. אם כך, עולה השאלה מהי סטיית תקן ולמה משתמשים בה?
סטיית תקן היא למעשה השורש של שונות. בדומה לשונות, גם סטיית תקן היא מדד פיזור אשר מטרתו להעיד על ממוצע המרחקים מהממוצע. כלומר בדוגמה לעיל, סטיית התקן שווה ל-1.63.
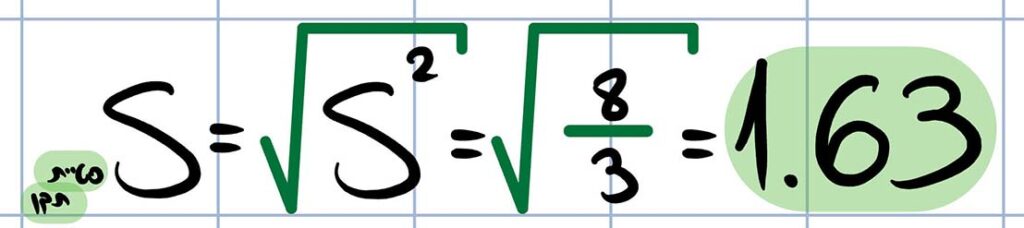
משתמשים בה ולא בשונות מכיוון שהיא הרבה יותר נוחה לשימוש וכפועל יוצא, מרבית הנוסחאות בסטטיסטיקה משלבות סטיית תקן ולא שונות.
נקודה למחשבה: קודם לכן, בחרנו סדרת ערכים פשוטה שהשונות בה יצאה נמוכה מאוד. מה לדעתכם היה קורה אם היינו מנסים לחשב שונות למשתנה כמו שכר?
במקרה כזה, השונות הייתה גבוהה מאוד והיה קשה לעבוד עמה. פעולת השורש שבאמצעותה מחושבת סטיית התקן נועדה להפוך את השונות למספר נוח יותר לשימוש על ידי החזרתו לגדלי ערכיו המקוריים (פעולה זו הינה למעשה הפעולה ההפוכה לפעולת ההעלאה בריבוע שערכנו קודם לכן לסטיות מהממוצע כדי להפוך אותם לחיוביים).
סטיית תקן מדגמית לעומת סטיית תקן באוכלוסייה
בתיכון ובקורס מבוא לסטטיסטיקה או סטטיקה א’, כאשר מלמדים סטטיסטיקה תיאורית, מלמדים לחשב שונות סטטיסטיקה על פי הנוסחה:
הערה: מי שאינו יודע מהו הסימן Σ, שמו הוא סיגמא וניתן ללחוץ כאן כדי לקרוא על תפקידו בהרחבה בהקשר לנוסחת סטיית תקן ובכלל.
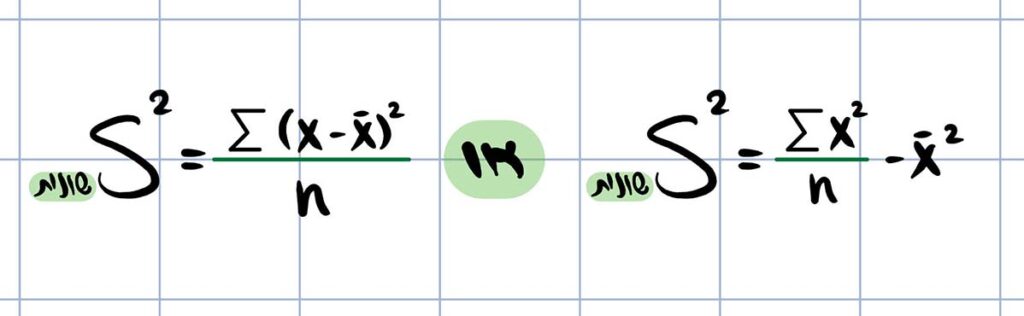
ואז כל שנותר הוא להוציא שורש ולקבל את סטיית תקן נוסחה
זוהי למעשה הנוסחה לחישוב סטיית התקן של האוכלוסייה מכיוון שהחישוב נעשה כדי לחשב את הפיזור של סדרת הערכים הנוכחית ללא התייחסות לאוכלוסייה כללית גדולה יותר. כלומר, באופן תיאורטי, סדרת הערכים עליה נבצע את החישוב מהווה את האוכלוסייה כולה.
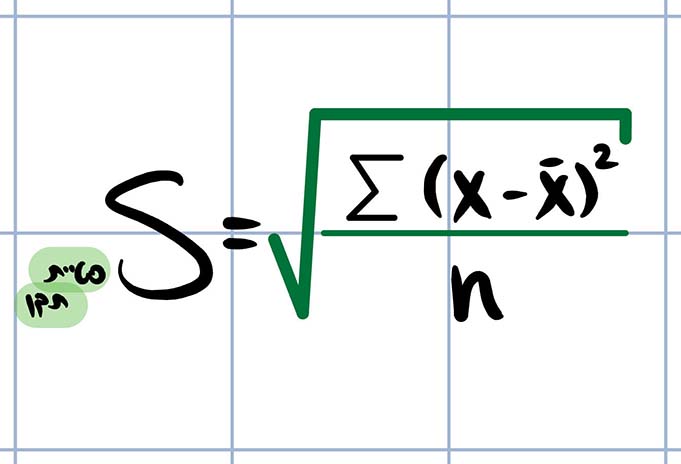
הערה חשובה: הצגנו לעיל כי האות המסמנת סטיית תקן זו היא S. זהו הסימון הנכון בקורסים הבסיסיים בהם לומדים סטטיסטיקה אולם סימון זה משתנה ל- σ, המכונה סיגמא (נכון- אותו השם כמו Σ אך משמעותו אחרת לגמרי), כאשר מתחילים ללמוד על קיומה של אוכלוסייה בקורסים מתקדמים יותר.
בסטטיסטיקה מתקדמת שלומדים במסגרת הקורסים סטטיסטיקה ב’, רגרסיה וניתוחי שונות ובמחקר כמותי בכלל, מחשבים את סטיית התקן המדגמית מתוך הניסיון להסיק על סטיית התקן של האוכלוסייה, כפי שנהוג בסטטיסטיקה היסקית.
סטיית התקן המדגמית, או בשמה השני סטיית תקן מתוקנת, מחושבת באופן כמעט זהה אולם שונה בסימנה ובמשמעותה. איך מוצאים סטיית תקן מדגמית? נוסחת החישוב היא:
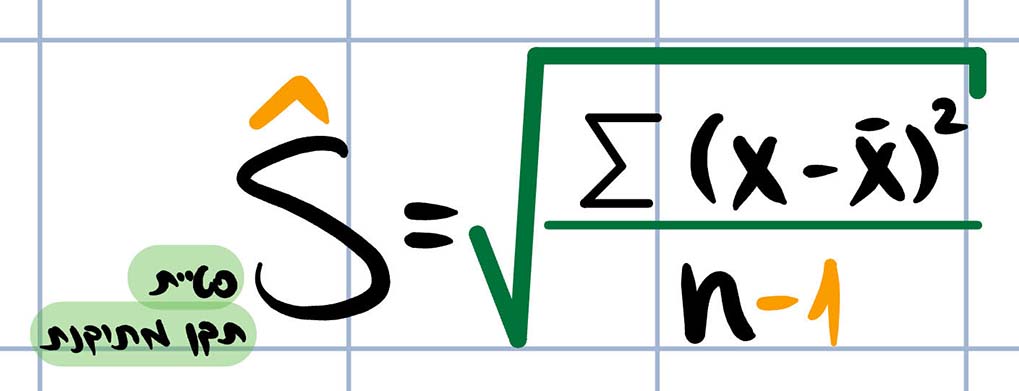
כפי שניתן לראות, מונה הנוסחה נותר זהה אולם למכנה התווסף הערך 1-. מצב זה נובע מכך שמתמטית, סטיית התקן המדגמית שממנה ננסה להסיק על זו של האוכלוסייה, נוטה להיות קטנה יותר מזו של האוכלוסייה ועל כן יש לתקנה על ידי החסרה של 1 מהמכנה. זוהי למעשה סטיית התקן שמחשבים בכל פעם שמנסים להסיק מן המדגם לאוכלוסייה ונקראת – S כובע.
סטיית תקן התפלגות נורמלית
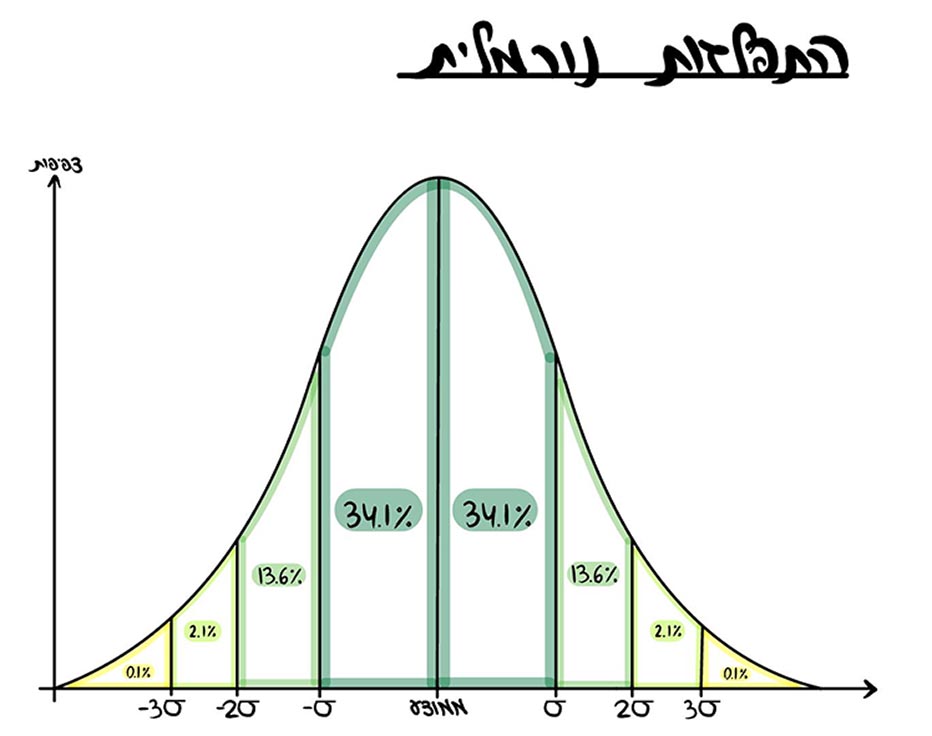
סטיית תקן היא הסטייה הממוצעת בין ערכי המשתנה לממוצע ההתפלגות. בהתפלגות נורמלית, כ-68% מהערכים נמצאים בטווח של סטיית תקן מעל ומתחת לממוצע ואילו 95% (68%+27%) נמצאים בטווח של שתי סטיות תקן מעל ומתחת לממוצע.
בהתפלגות נורמלית נהוג להשתמש בסטיית התקן על מנת לחשב ציון תקן, וזאת בכדי לחשב הסתברות למאורע מסוים. למשל, הסיכוי לקבל ערך הגבוה ב-3 סטיות תקן מהממוצע בהתפלגות נורמלית הוא 0.001 או 0.1%.
מהי המשמעות של סטיות תקן ולמה הן משמשות?
ניתן לומר, וכנראה שכמעט ובלי להגזים, שסטיית תקן היא הביטוי הכי נפוץ ושימושי בסטטיסטיקה לאחר ממוצע. כמדד פיזור, היא מאפשרת לתאר את המידה שבה התפלגות נתונים מפוזרת. במילים אחרות, סטיית תקן קטנה מצביעה על כך שערכי ההתפלגות קרובים לממוצע, בעוד שסטיית תקן גדולה מצביעה על כך שערכי ההתפלגות מפוזרים יותר, כך שהערכים שונים מאוד האחד ממשנהו.
סטיית תקן משמשת בדרך כלל בתחומים רבים, לרבות כלכלה, הנדסה ומדעי החברה, בכדי לכמת את מידת הגיוון או אי הוודאות בנתונים. כך למשל, אם נתקל במניה (Stock) עם סטיית תקן גדולה יחסית בשוק ההון, נוכל להבין כי תנודותיה גדולות ונבינה כבעלת פוטנציאל צמיחה גדול אך גם כמסוכנת יותר ממניה אחרת בעלת סטיית תקן קטנה יותר, שתחשב לעומתה ליציבה.
להלן מספר שימושים נוספים בתחום האקדמיה והמחקר:
- השוואת שתי התפלגויות או יותר: מבחנים סטטיסטיים אשר בוחנים הבדלים בין קבוצות אמנם מתייחסים להבדלים במדדי המרכז (לדוגמה, ממוצע), אולם לוקחים בחשבון גם מדדי פיזור כדוגמת סטיית התקן. למשל, אם מבחן סטטיסטי שיבחן את ההבדל בשביעות הרצון מהזוגיות בין גברים לנשים ימצא כי ממוצע הגברים עומד על 3.5 ואילו בקרב נשים הממוצע הוא 4. היות שישנה סטיית תקן גדולה בקרב אוכלוסיית הנשים (דהיינו, הבדלים ניכרים בין הנשים השונות באוכלוסייה) בהשוואה לאוכלוסיית הגברים, לא ימצא הבדל משמעותי בין גברים לנשים בשביעות הרצון מהזוגיות. היעדר ההבדל המובהק נובע מכך שייתכן והממוצע של הנשים גבוה משום שיש נשים שמביעות שביעות רצון גבוהה מאוד מהזוגיות ובכך מגדילות את הממוצע באופן שמקשה על ההסקה לגבי כלל אוכלוסיית הנשים. שימו לב כי רק כאשר התייחסנו לסטיית התקן יכולנו לבחון את ההבדלים בין ממוצעי הקבוצות.
- הערכת התקינות של מערך נתונים (Data): ניתן להשתמש בסטיית תקן בשילוב בדיקות סטטיסטיות אחרות כדי להעריך אם מערך הנתונים מתפלג נורמלית. מרבית המבחנים הסטטיסטיים המוכרים מניחים שהתפלגות הדגימה נורמלית וללא צורה זו של ההתפלגות יש לבצע ניתוחים סטטיסטיים פחות מוכרים המכונים מבחנים א-פרמטריים.
- זיהוי ערכים חריגים (Outliers): ניתן להשתמש בסטיית תקן כדי לזהות האם בהתפלגות המשתנים ישנם ערכים חריגים. ערכים חריגים עלולים להשפיע על הניתוחים הסטטיסטיים וכפועל יוצא על יכולתנו להסיק מסקנות מדויקות במחקרנו.
דרכים פשוטות לחישוב סטיית תקן
קיימות מספר דרכים פשוטות לחישוב סטיית התקן מלבד השיטה הידנית הנהוגה בקורסי הסטטיסטיקה.
סטיית תקן באקסל
אחת הדרכים הנגישות היא לחישוב סטיית תקן אקסל. קיימת אפשרות לחישוב סטיית תקן של האוכלוסייה (הנתונים הינם כלל הנתונים ואין ניסיון להסיק מהם על אוכלוסייה רחבה יותר) או סטיית תקן מדגמית (הנתונים מדגמיים וישנו ניסיון להסיק מהם על האוכלוסייה הכללית).
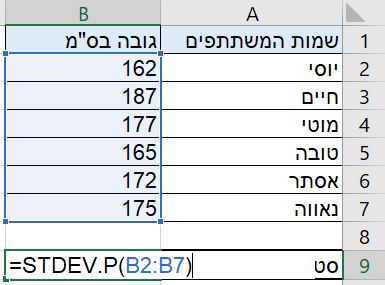
חישוב סטיית תקן של האוכלוסייה תבוצע באמצעות הפקודה: STDEV.P
נבחר בתא שבו יוצג חישוב סטיית התקן ונקליד בו את הביטוי: )STDEV.P=
לאחר מכן נקיף (או נקליד ידנית) את כל הערכים שעליהם נבקש לחשב את סטיית התקן ונסיים בסגירת הסוגריים (
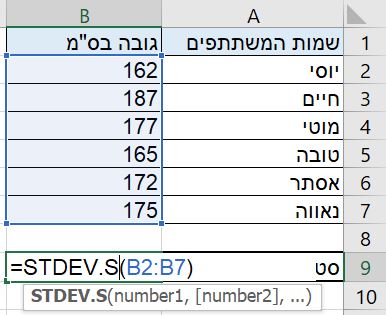
לעומת זאת, חישוב סטיית תקן מדגמית תבוצע באמצעות הפקודה: STDEV.S
שימו לב: האות P מסמנת את המילה Population (אוכלוסייה) ואילו S את המילה Sample (מדגם). כמו כן, חישוב סטיית התקן המדגמית תמיד תוביל לערך גבוה יותר בהשוואה לחישוב סטיית התקן של האוכלוסייה כפועל יוצא של הנוסחאות השונות לחישוב.
פרוצדורת חישוב שונות באקסל תבוצע באופן דומה, כאשר הפקודות הן: VAR.P= או VAR.S=, בהתאמה.
חישוב סטיית תקן באינטרנט
ישנם מספר מחשבונים אינטרנטיים שנועדו להקל על מהלך חישוב סטיית תקן במצבים שאין ברשותנו אפשרות לגשת לתוכנות מובנות. אחד מהאתרים המומלצים בתחום בו תוכלו למצוא מחשבון לסטיית תקן הוא של אתר Socstatistics.com:
יש להקליד את סדרת הערכים כאשר בין ערך לערך יש ללחוץ על הלחץ “Enter” במקלדת, לבחור אם מעוניינים לחשב סטיית תקן עבור אוכלוסייה (Population) או מדגם (Sample) וללחוץ על כפתור ה-Calculate.

חישוב סטיית תקן ושונות בתוכנות סטטיסטיות כדוגמת SPSS
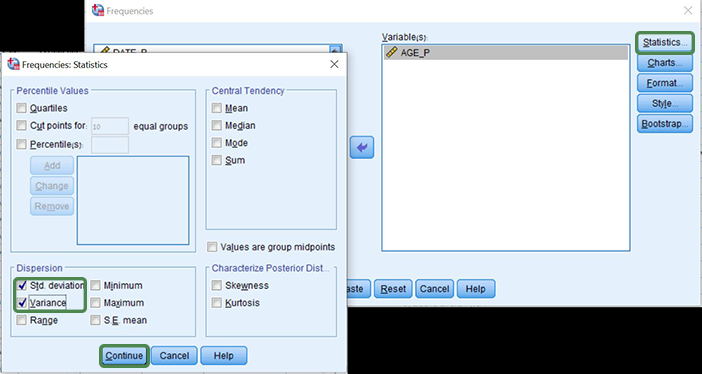
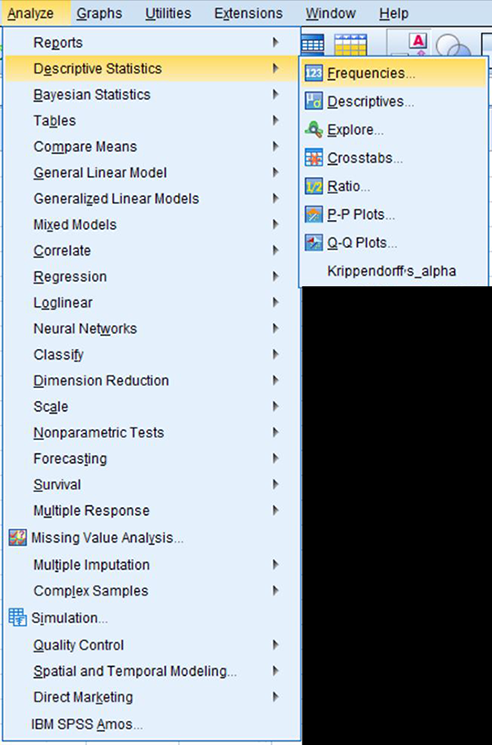
לשם חישוב באמצעות שונות וסטיית תקן באמצעות SPSS יש לפתוח קובץ נתונים ובו משתנה כמותי. לאחר מכן יש לבחור את סדרת הפעולות הבאה:
לאחר מכן יש לעביר לחלון הימני את המשתנה עליו נרצה לבצע את החישוב, ללחוץ Statistics ולסמן את Std. deviation (סטיית תקן) ו-Variance (שונות):