במאמר שלהלן נבהיר מהי התפלגות דגימה וכיצד היא שונה מהתפלגויות מוכרות אחרות כדוגמת התפלגות האוכלוסייה והתפלגות המדגם. כמו כן, נמחיש כיצד נראית ההתפלגות ומהם מאפייני התפלגות הדגימה של הממוצע והתפלגות הדגימה של הסכום.
תוכן עניינים

סטטיסטיקה עוסקת בשלושה סוגי התפלגויות עיקריים: התפלגות אוכלוסייה, התפלגות מדגם והתפלגות דגימה. נתחיל משתי ההתפלגויות הבסיסיות, התפלגות האוכלוסייה והתפלגות המדגם, על מנת להבין מהי התפלגות הדגימה.
התפלגות האוכלוסייה (Population distribution)
התפלגות האוכלוסייה עוסקת באופן שבו המשתנה מתפלג באוכלוסייה, למשל כיצד המשתנה גובה מתפלג באוכלוסיית מדינת ישראל. בדוגמה זו גובה יתפלג עם ממוצע מסוים (μ, נהגית כ-Miu) וסטיית תקן מסוימת (σ ,נהגית כ-Sigma). צורת התפלגות האוכלוסייה יכולה להיות נורמלית (פעמונית), א-סימטרית ימנית (חיובית) או שמאלית (שלילית), אחידה וכיוצא בזאת. בהתפלגות זו יכללו כלל התצפיות באוכלוסייה, כלומר כל נקודה בהתפלגות תסמן תצפית מתוך האוכלוסייה הכללית. להלן שתי סוגי התפלגויות להמחשה:
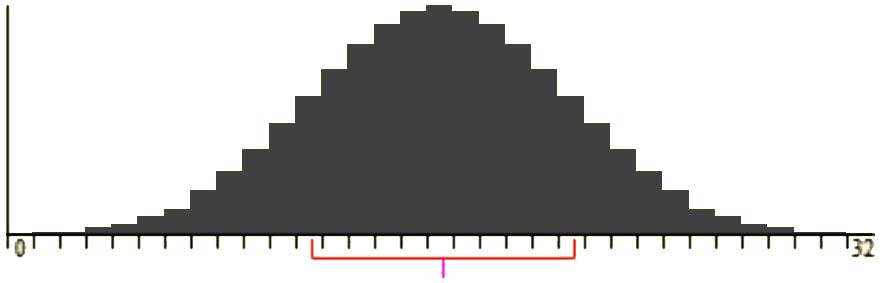
(Sampling Distribution, n.d)
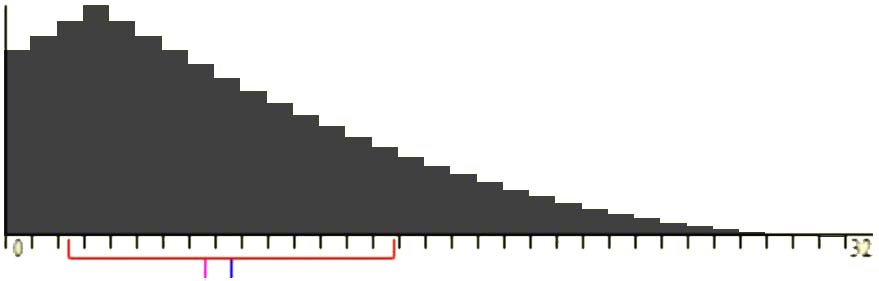
התפלגות המדגם (Sample distribution)
לעומת התפלגות האוכלוסייה, התפלגות המדגם מתייחסת אך ורק לאופן ההתפלגות של מדגם מסוים שנלקח מתוך האוכלוסייה בדגימה אחת כלשהי. למשל התפלגות מדגם ערכי הגובה של 25 תלמידי תיכון שנדגמו מתוך אוכלוסיית תלמידי התיכון במדינת ישראל. במקרה זה, המשתנה גובה במדגם יתפלג עם ממוצע (x̅) וסטיית תקן (S). נתונים אלו אשר מתארים את התפלגות המדגם, נקראים סטטיסטיים ונועדו לאפיין מדגם נתון.
על מנת להמחיש כיצד נראית התפלגות מדגם בהשוואה להתפלגות האוכלוסייה, מוצגת להלן התפלגו המורכבת מ-16 בלוקים שחורים אשר מסמלים 16 תצפיות שנדגמו באופן מקרי מתוך האוכלוסייה הכללית:
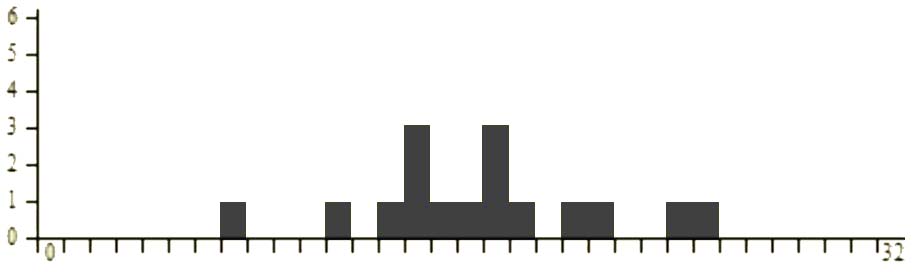
(Sampling Distribution, n.d)
לצד שתי התפלגויות חשובות אלו, קיימת התפלגות חשובה במיוחד לעולם המחקר המכונה התפלגות הדגימה.
התפלגות הדגימה
התפלגות הדגימה היא התפלגות תיאורטית אשר מתייחסת למצב היפותטי שבו חוקר דוגם אינסוף מדגמים באותו הגודל (למשל אינסוף מדגמים בגודל 16). החוקר משתמש במדד סטטיסטי מסוים עבור כל מדגם מתוך אינסוף המדגמים, פעם אחר פעם, עד אשר נוצרת ההתפלגות חדשה – התפלגות הדגימה. חשוב לציין כי סטטיסטיים שונים (ממוצע, חציון, סכום, סטיית תקן) יובילו להתפלגויות דגימה שונות מתוך אותה אוכלוסייה. התפלגות הדגימה הנפוצה ביותר במחקר ובאקדמיה בכלל היא התפלגות הדגימה של הממוצע.
התפלגות הדגימה של הממוצע
היות שהתפלגות הדגימה של הממוצע הוא ביטוי ארוך ומסורבל, לרב נוטים לקצרו ופשוט לציין את חלקו הראשון – התפלגות הדגימה (כלומר לא מציינים שזו התפלגות הדגימה של הממוצע כיוון שזו ההתפלגות הנפוצה ביותר). בהתפלגות זו, כל ממוצע של מדגם מהווה מעין תצפית בתוך התפלגות הדגימה.
כלומר, בהתפלגות שניתן לראות להלן, מוצגת התפלגות הבנויה מבלוקים כחולים. כל בלוק כחול מהווה למעשה ממוצע של מדגם אחד מתוך אינסוף המדגמים שנדגמו.
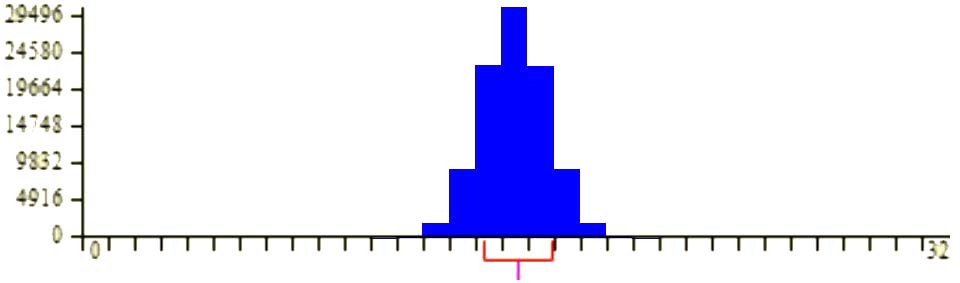
(Sampling Distribution, n.d)
הערה חשובה: כפי שצוין לעיל, זוהי התפלגות תיאורטית ולכן חוקר לעולם לא יוכל להגיע אליה. למעשה, החוקר אף פעם אינו חשוף הן להתפלגות האוכלוסייה והן להתפלגות הדגימה. להתפלגות האוכלוסייה החוקר אינו חשוף שכן במידה והיה, לא היה זקוק לסטטיסטיקה על מנת להסיק מסקנות (שהרי יכול לומר בדיוק מה יקרה או מה קרה). לעומתה, החוקר אינו לא יכול להיחשף להתפלגות הדגימה מאחר שלשם כך הוא זקוק לדגימת אינסוף מדגמים וזה כמובן מצב בלתי אפשרי.
למעשה, התועלת המרכזית של התפלגות הדגימה היא כדי שנוכל לערוך ניתוחים סטטיסטיים במטרה להסיק על התפלגות האוכלוסייה. לפיכך והיות שהיא תיאורטית, אין באמת צורך להגיע לכדי התפלגות זו.
ממוצע התפלגות הדגימה שווה לתוחלת האוכלוסייה
כפי שהוסבר לעיל, כל תצפית בהתפלגות הדגימה מהווה ממוצע מדגם אחד מתוך אינסוף המדגמים שנדגמו. יוצא אפוא שהממוצע של התפלגות הדגימה נקרא ממוצע הממוצעים (נכתב כ-X גגיים, x̅ עם גג נוסף מעליו) ומהווה את הממוצע של אינסוף המדגמים שנדגמו. מאמר זה לא יכסה את ההוכחה המתמטית המסבירה כיצד ממוצע ממוצעי התפלגות הדגימה שווה לתוחלת האוכלוסייה אולם ימחיש זאת באמצעות הדגמה קצרה:
היות שאנחנו מתייחסים להתפלגות אינסופית אשר במסגרתה נדגמים כל המדגמים האפשריים בגודל מסוים מתוך כלל האוכלוסייה, נדמה מצב כזה בעבור אוכלוסיית משתנה כשלהו שערכיו הם 1,3,5.
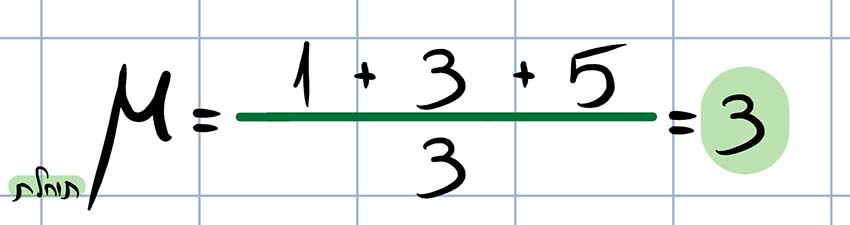
על פי חישוב תוחלת (שיוצא כמו חישוב ממוצע במקרה לעיל) משתנה זה יתפלג עם תוחלת 3:
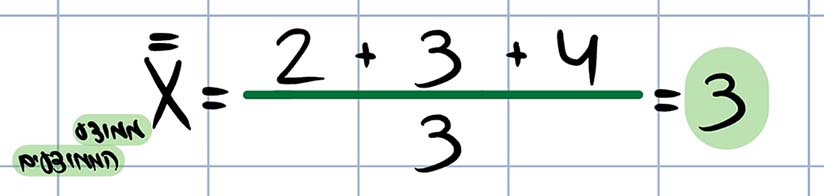
לצורך ההמחשה נניח שהחוקר החליט לדגום מדגם בגודל 2 (n=2) ולפיכך ידגום שני ערכים מתוך כלל האוכלוסייה שמורכבת משלושת הערכים 1,3,5. כלל אפשרויות המדגם שלו הן 1,3 , 1,5, ו-3,5 כאשר נוכל לראות שהממוצעים של זוגות התצפיות בכל מדגם הם 2, 3, ו-4 בהתאמה. אם כך, ניתן לראות כי ממוצע הממוצעים של התפלגות הדגימה שווה גם הוא ל-3:
טעות התקן, סטיית התקן של התפלגות הדגימה
כמו כל חישוב של ממוצע, השונות הממוצעת (השונות של התפלגות הדגימה), מחושבת על ידי חלוקת שונות האוכלוסייה בגודל המדגם ותראה כך:
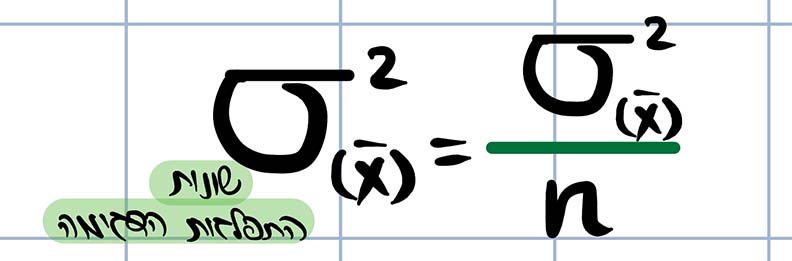
מאחר וסטיית התקן הינה שורש השונות, כדי לקבל את סטיית התקן של התפלגות הדגימה (Standard deviation of sampling distribution), המכונה גם טעות התקן (Standard error או בקיצור SE) נוציא שורש לשונות, הן למונה והן למכנה, ונקבל את הביטוי:

אם נתחבר שוב לדוגמה הקודמת על משתנה כלשהו שערכיו באוכלוסייה הם 1,3,5- סטיית התקן של משתנה זה באוכלוסייה תהיה:

לעומת זאת, טעות התקן תהיה:
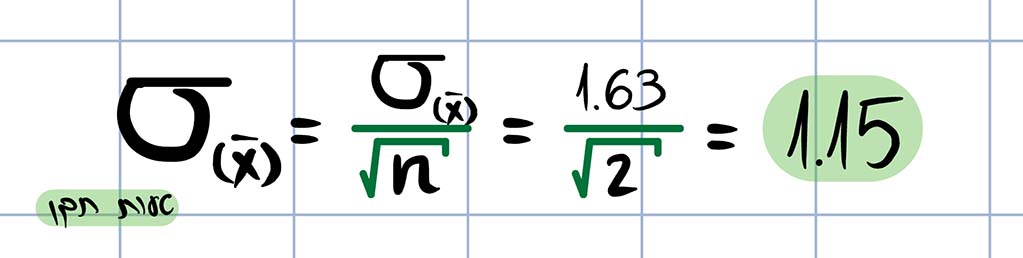
הערה חשובה: תמיד טעות התקן תהיה קטנה מאשר סטיית התקן של האוכלוסייה. למעט במצבים שבהם גודל המדגם הוא 1, כלומר שבכל דגימה החוקר דוגם תצפית אחת בלבד (n=1) שהרי אז התפלגות האוכלוסייה והתפלגות הדגימה יהיו זהות. מצב זה גורם לכך שהתפלגות הדגימה תמיד תהיה צרה יותר מהתפלגות האוכלוסייה (כשם שניתן לראות בתמונות).
התפלגות הדגימה של הסכום
התפלגות הדגימה של סכום התצפיות היא מקרה פחות שכיח של התפלגות הדגימה והינה מצב היפותטי ובו נדגמים אינסוף מדגמים באותו הגודל (למשל אינסוף מדגמים בגודל 100) אך שבמקום שממוצע כל אחד מהמדגמים ישמש כתצפית בהתפלגות הדגימה, סכום הערכים בכל אחד מהמדגמים משתמש כתצפיות ההתפלגות. במידה והתפלגות האוכלוסייה נורמלית, ממוצע התפלגות הדגימה הוא ממוצע סכומי אינסוף המדגמים והוא מתפלג עם ממוצע של וטעות תקן של . חשוב לציין כי יכולה להיות התפלגות דגימה עבור כל סטטיסטי שהוא, כולל התפלגות דגימה של סטיית תקן, חציון, פרופורציה ועוד.
מה השימושים של התפלגות הדגימה וטעות תקן?
התפלגות הדגימה הינה כלי מרכזי בסטטיסטיקה לשם בדיקת השערות. למעשה, על אף שמעט זמן במהלך הקורס מוקדש ללמידת התפלגות הדגימה, היא מהווה את הבסיס להסקת מסקנות בנוגע להשערות מחקר בסטטיסטיקה היסקית. למעשה, כל המבחנים הפרמטריים (מבחן Z, מבחן T, אנובה ועוד) מתבססים על התפלגות הדגימה בפרוצדורה של בדיקת השערות.
דוגמה לכך ניתן לראות בנוסחה לחישוב ציון התקן (Z) שהינו הערך הסטטיסטי:
x̅ מייצג את ממוצע המדגם שדגם החוקר.
μ (תוחלת) מייצגת את ממוצע האוכלוסייה, אשר כפי שהוצג לעיל, שווה לממוצע הממוצעים של התפלגות הדגימה.
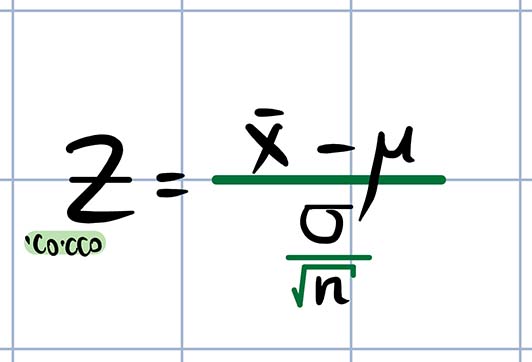
יתרה מזאת, טעות התקן הינה הבסיס לפרוצדורות סטטיסטיות נוספות כדוגמת אמידה באמצעות רווח סמך ומבחני בדיקת השערות נוספים כמו רגרסיה.
ביבליוגרפיה
Sampling Distribution. (n.d.). Online Statistics Education. https://onlinestatbook.com/stat_sim/sampling_dist/
הופק באמצעות מכונת הציטוטים
